티스토리 뷰
728x90
참고 자료
- 재학 대학의 '자료구조' 수업 자료
- 「Do it! 자료구조와 함께 배우는 알고리즘 입문 파이썬 편」 시바타 보요 지음
- 「2023 정보처리기사 필기 핵심 요약」 시나공
- (44) 코딩 테스트를 위한 트리(Tree) 자료구조 10분 핵심 요약 - YouTube
내용 구성
- 트리란?
- 트리 관련 용어
- 이진 트리
- 이진 트리의 종류
- 편향 트리
- 포화 이진 트리
- 완전 이진 트리
1. 트리란?

트리는 사이클이 존재하지 않는 그래프의 특수한 형태이다. 데이터를 1:N의 계층적인 구조로 나타내는 자료구조로, 대표적으로 가계도가 그 예이다.
2. 트리 관련 용어

- 서브 트리: 하나의 트리에 속하는 또 다른 트리
- 위 그림에서 주황색 삼각형이 서브 트리이다.
- 루트 노드: 트리의 최상단 노드로, 부모 노드가 없다.
- A (주황색 노드)
- 단말 노드: 트리의 최하단 노드로, 자식 노드가 없는 노드이다.
- D, E, F, G (초록색 노드)
- 부모 노드: 어떤 노드와 연결된 이전 레벨의 노드
- B, C, D의 부모 노드는 A
- 자식 노드: 어떤 노드와 연결된 다음 레벨의 노드
- B의 자식 노드는 E와 F
- 형제 노드: 같은 부모 노드를 갖는 노드들
- B라는 같은 부모 노드를 가지는 E와 F는 형제 노드
- 노드의 크기: 자신을 포함한 모든 자식 노드의 개수
- A 노드의 크기: 7, C 노드의 크기: 2
- 노드의 깊이: 루트 노드로부터 해당 노드까지 도달하기 위한 간선의 수
- B 노드의 깊이: 1
- 노드의 레벨: 해당 노드가 위치한 레벨
- B, C, D의 레벨: 2
- 노드의 차수(Degree): 해당 노드의 서브 트리 개수 (= 자식 노드 개수)
- A의 차수: 3, B의 차수: 2, C의 차수: 1
- 트리의 크기: 트리에 속한 모든 노드의 개수
- 트리의 크기: 7
- 트리의 차수: 트리에 속한 노드의 최대 차수
- 트리의 차수: 3
- 트리의 높이(깊이): 트리에 속한 노드의 최대 레벨
- 트리의 높이: 3
3. 이진 트리

이진 트리는 트리에 속한 각 노드의 차수가 최대 2인 트리이다. 즉, 모든 노드가 왼쪽 자식 노드와 오른쪽 자식 노드 중에서 (1) 아무 자식이 없거나 (2) 왼쪽만 있거나 (3) 오른쪽만 있거나 (4) 왼쪽과 오른쪽이 모두 있는 상황 중에 하나인 것이다.
노드 A의 왼쪽 자식은 노드 B이고, 오른쪽 자식은 노드C이다. 이때 왼쪽 자식인 노드 B를 루트 노트로 갖는 서브 트리는 노드 A의 왼쪽 서브 트리이고, 오른쪽 자식 노드 C를 루트 노드로 갖는 서브 트리는 오른쪽 서브 트리이다.
- 이진 트리의 성질
- 트리의 크기가 N일 때 최악의 경우 이진 트리의 높이는 N이다.
- 이진 트리의 레벨i에서의 최대 노드 수는 2 ^ (i - 1) (i ≥ 1)이다.
- 깊이가 k인 이진 트리가 가질 수 있는 최대 노드의 개수는 2 ^ (k - 1) (k ≥ 1)이다.
4. 이진 트리의 종류
- 편향 이진 트리 (Skewed Binary Tree)

편향 트리는 오직 왼쪽이나 오른쪽 서브 트리만 존재하는 트리이다.
- 포화 이진 트리 (Full Binary Tree)
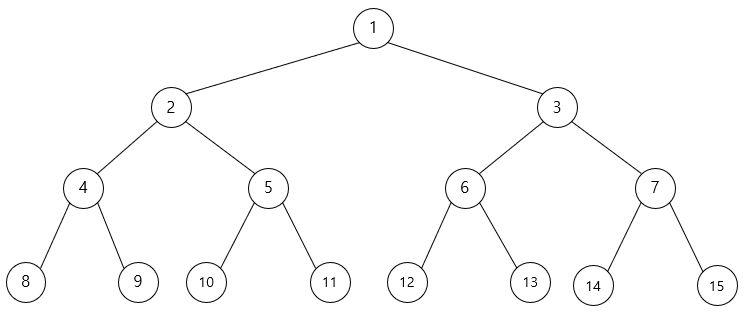
트리의 각 레벨에 존재할 수 있는 모든 노드가 꽉 찬 이진 트리이다.
트리의 높이가 k일 때 노드의 개수는 2^(k - 1)이다.
- 완전 이진 트리 (Complete Binary Tree)

트리의 높이가 k일 때 레벨1 ~ 레벨k - 1까지는 포화 이진 트리처럼 모든 노드로 꽉 차 있지만, 마지막 레벨에서는 노드가 왼쪽부터 순서대로 채워져 있는 형태이다. (마지막 레벨 역시 노드로 꽉 채워질 수도 있다.)
728x90
