티스토리 뷰
https://www.acmicpc.net/problem/15686
15686번: 치킨 배달
크기가 N×N인 도시가 있다. 도시는 1×1크기의 칸으로 나누어져 있다. 도시의 각 칸은 빈 칸, 치킨집, 집 중 하나이다. 도시의 칸은 (r, c)와 같은 형태로 나타내고, r행 c열 또는 위에서부터 r번째 칸
www.acmicpc.net

1. 접근 방식
- 치킨 집과 가정 집의 좌표를 원소로 갖는 리스트를 각각 생성하자
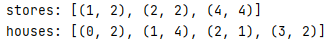
치킨 거리를 구하는 방법이 치킨 집과 가정 집의 좌표로 구해지므로, 이 문제에서 필요한 것은 오직 치킨 집과 가정 집의 위치 정보다.
그리고 여러 개의 치킨 집 중에서 m개만 뽑는 조합(nCm)을 구해야 하는데, 치킨 집의 인덱스를 가지고 각 조합을 표현할 예정이므로 리스트를 생성해야 한다.
- 2차원 배열에 모든 치킨 집과 가정 집의 거리를 저장하자
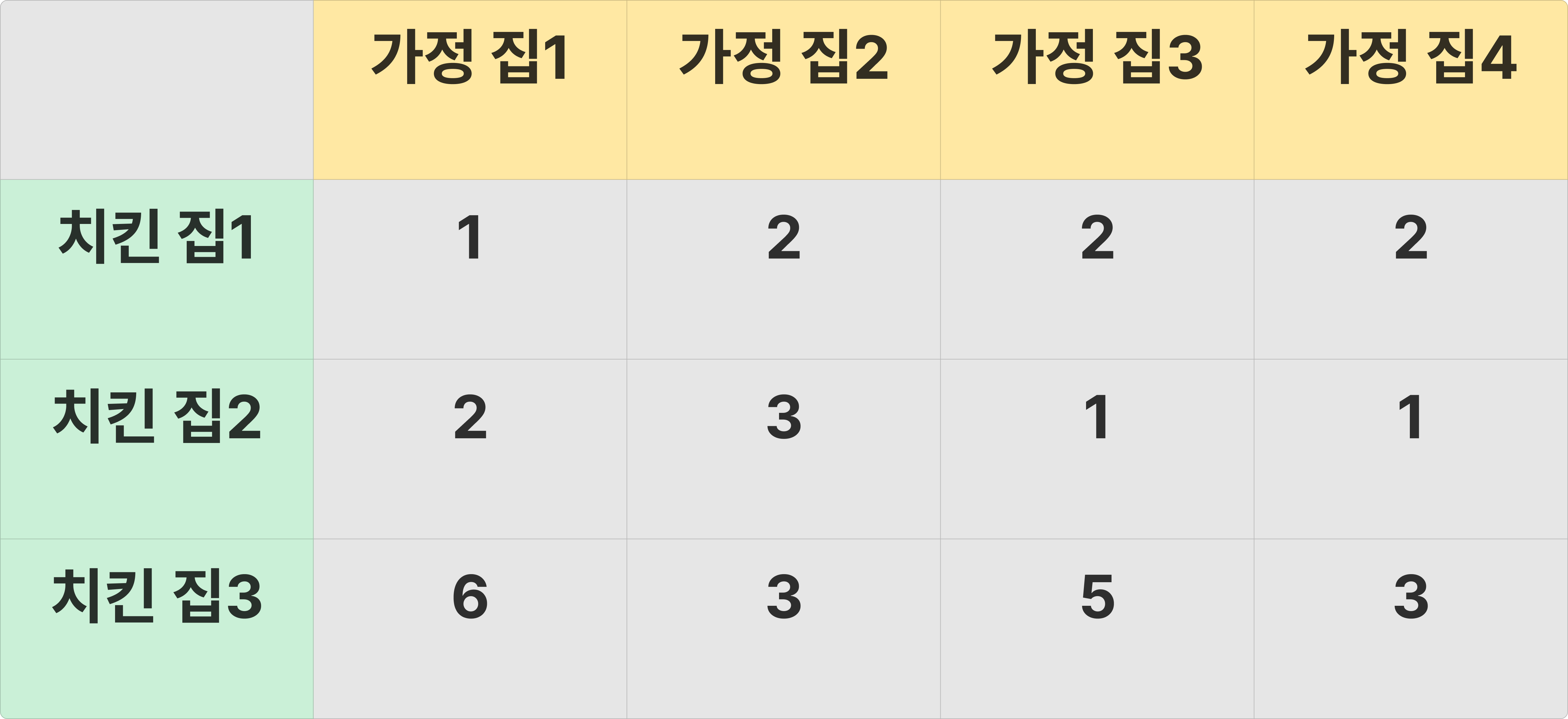
어떤 치킨 집 조합이 1, 2, 3일 때, 어느 가정 집에서 어떤 치킨 집이 가장 가까운지를 알아내기 위해서는 치킨 집 1, 2, 3과 가정 집의 거리를 모두 계산해서 비교해야 한다. 따라서 아예 각 치킨 집과 각 가정 집의 모든 경우의 수를 표현할 수 있는 2차원 배열에 치킨 거리를 저장해두자.
참고로 위 그래프에서 치킨 집1과 가정 집3의 치킨 거리는 2이고, 치킨 집2와 가정 집3의 치킨 거리가 1이라는 의미이다.
- 가능한 치킨 집의 조합를 구하자
치킨 집이 3개가 있을 때 M이 2라면 3개의 치킨 집 중에 2개만 선택해야 한다. 이때 (치킨 집1, 치킨 집2)와 (치킨 집2, 치킨 집1)은 동일한 결과를 나타내므로, (1, 2), (1, 3), (2, 3)이라는 결과를 얻을 수 있도록 조합을 구해야 한다.
모든 조합별로 위에서 생성한 그래프를 활용해 각 최단 치킨 거리를 구한다. 그 중 가장 작은 값이 최단 치킨 거리, 즉 정답이다. 예를 들면 치킨 집 (1, 2) 조합의 최단 치킨 거리가 5, (1, 2)는 7, (2, 3)은 7일 때, 이중 가장 값이 작은 5가 정답이 되는 것이다.
2. 정답 코드
- dfs 함수의 종료 조건에서 combinations에 원소를 추가할 때 copy()를 하지 않으면, 리스트의 참조만 넘기기 때문에 이후 combination 리스트가 변경되면 combinations에 추가된 모든 하위 리스트도 변경되게 된다. 따라서 반드시 combination.copy()를 통해 복사본을 append해야 한다.
import sys
input = sys.stdin.readline
INF = 99999
def get_path_graph():
graph = [[] for _ in range(stores_n)] # row: store, col: house
for s in range(stores_n):
for h in range(houses_n):
graph[s].append(abs(stores[s][0] - houses[h][0]) + abs(stores[s][1] - houses[h][1]))
return graph
def dfs(depth, index, combination):
if depth >= M:
combinations.append(combination.copy())
return
for s in range(index, stores_n):
combination.append(s)
dfs(depth + 1, s + 1, combination)
combination.pop()
def solve():
answer = INF
for combination in combinations:
result = [INF] * houses_n
for s in combination:
for h in range(houses_n):
result[h] = min(result[h], path_graph[s][h])
answer = min(answer, sum(result))
return answer
# main
N, M = map(int,input().split())
stores = []
houses = []
stores_n = 0
houses_n = 0
for i in range(N):
row = list(map(int, input().split()))
for j in range(N):
if row[j] == 2:
stores.append((i, j))
stores_n += 1
elif row[j] == 1:
houses.append((i, j))
houses_n += 1
path_graph = get_path_graph()
combinations = []
dfs(0, 0, [])
print(solve())'코딩 테스트 > 백준' 카테고리의 다른 글
| [백준] 14503번 로봇 청소기 파이썬 풀이 (0) | 2024.03.15 |
|---|---|
| [백준] 14502번 연구소 파이썬 정답 풀이 (0) | 2024.03.14 |
| [백준] 2294번 동전 2 파이썬 정답 풀이 (0) | 2024.03.09 |
| [백준] 1890번 점프 파이썬 풀이 (0) | 2024.03.08 |
| [백준] 17144번 미세먼지 안녕! 파이썬 정답 풀이 (0) | 2024.03.08 |
